La méthode de Lagrange

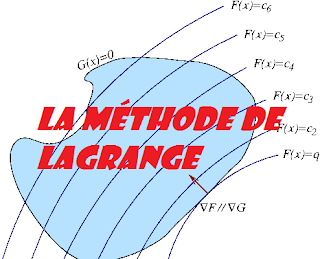
Le multiplicateur de Lagrange est une méthode permettant de trouver les points stationnaires (maximum, minimum...) d’une fonction dérivable d’une ou plusieurs variables, sous contraintes. Visuellement, la méthode des multiplicateurs de Lagrange permet de trouver un optimum, sur la figure ci-dessous le point le plus élevé possible, tout en satisfaisant une contrainte, sur la figure un point de la ligne rouge. Le théorème clé se conçoit aisément dans un exemple de dimension 2. Le point recherché est celui où la courbe rouge ni ne monte ni ne descend. Formellement, on note comme suit l’écriture du Lagrangien : L(x, λ) = ϕ(x) + λψ(x) avec x les variables de contrôle figurant dans la fonction à maximiser ou de minimiser, ϕ(x) est la fonction à optimiser, λ le multiplicateur de Lagrange et ψ(x) la contrainte du programme d’optimisation. 1 Le comportement du producteur Pour caractériser le comportement du producteur, l’analyse microéconomique suppose que l’objectif principal de ce dernier consiste à rendre son profit maximal. Le profit étant définit comme la différence entre le chiffre d’affaire et les coûts, il s’écrit mathématiquement : avec p le prix du bien ou service produit, pQ(K, L) le chiffre d’affaire, et −wL − rK − f les coûts et plus exactement wL le coût du travail, rK le coût du capital et f la rémunération de l’ensemble des facteurs fixes de l’entreprise. Rappel : Fonction de production : relation technique qui indique à partir de la quantité de facteurs mis en oeuvre par le producteur et la quantité maximale de produit qu’il peut obtenir. Le comportement du producteur peut alors être appréhendé de façon différentes selon qu’il rencontre ou non une contrainte sur la quantité à produire ou sur le coût qu’il peut supporter. (a) Le producteur contrait par son marché Supposons que le producteur connaît le niveau maximum de production qu’il peut écouler sur le marché, il est donc contraint par les quantités et connaît à l’avance le montant de sa recette pQ(K, L). Dans ce cas la max du profit implique la minimisation des coûts. Donc le problème du producteur se réduit à la recherche de l’utilisation optimale des facteurs de façon à minimiser= ses coûts de production. Le problème s’exprime mathématiquement sous la forme d’une minimisation de coûts sous la contrainte d’un niveau de production Q Le programme s’écrit alors : MinC(K, L) = wL + rK + f s.c Q(K, L) = Q La fonction de Lagrange correspondant à ce programme est : L(K, L, λ) = wL + rK + f − λ(Q(K, L) − Q) Les conditions du premier ordre, qui correspondent à l’annulation des dérivées premières sont données par : soit : r/w = QK /QL Avec QK et QL respectivement la productivité marginale du capital et du travail. Les deux premières équations du système des CPO permettent de définir la condition d’optimalité du producteur. (b) Le producteur contraint par son budget Le producteur peut se trouver dans une configuration alternative où il connaît son budget maximum. Les coûts ne pouvant excéder cette somme, le coût maximal de la production est connu et le recherche du profit le plus élevé possible passe par la maximisation de la recette. Le producteur va donc chercher la combinaison productive (K,L) qui maximise la volume de production tout en respectant la contrainte de coût. Le programme s’écrit : M ax Q(K, L) s.c C = wL + rK + f Le Lagrangien est alors : L(K, L, λ) = Q(K, L) + λ(C − rK − wL − f ) D’où d’après les CPO : soit : r/w = QK /QL Interprétation des conditions d’optimalité : La résolution des deux problèmes posés par le producteur permet d’établir qu’au point optimal, la rapport des prix des facteurs doit être égal au rapport des productivités marginales. Cette égalité s’explique simplement : la productivité marginale d’un facteur rapporté à son prix correspond à la production supplémentaire obtenue en consacrant une unité de compte à l’achat d’un facteur. Par conséquent, si cette égalité n’était pas vérifiée, reporter la dépense de cette unité de compte d’un facteur à l’autre permettrait de produire plus, ce qui signifierait que la combinaison initiale n’était pas optimale. 2 Le comportement du consommateur Le consommateur, s’il est est rationnel veut maximiser son utilité sous la contrainte d’un budget limité afin de déterminer les quantités x1 de bien 1 et x2 de bien 2 qu’il va demander. On suppose que l’utilité de l’agent ne dépend que des quantités de bien, ici x1 et x2. La contrainte de budget est donnée par : R = p1x1 + p2x2 avec R le revenu et p1x1 + p2x2 les dépenses. Le programme de maximisation s’écrit comme suit : M ax U (x1, x2) s.c R = p1x1 + p2x2 Nous avons précédemment résolu les programmes d’optimisation avec le Lagrangien, nous allons maintenant montrer qu’il est possible de raisonner autrement et de procéder à la méthode dite de substitution pour résoudre ce programme. (a) Méthode de substitution C’est une méthode qui consiste à transformer le programme de maximisation d’une fonction à deux variables sous contrainte en un programme de maximisation d’une fonction à une variable sous contrainte. La première étape consiste à exprimer une des variables en fonction de l’autre (par exemple x2 en fonction de x1) à partir de la contrainte Il faut ensuite le reporter dans la fonction d’utilité qui devient donc une fonction d’une seule variable (ici x1). On calcul ensuite les CPO pour trouver la valeur de x1 dU/dx1 = p1/p2 A l’optimum du consommateur le rapport des utilités marginales doit êtreégales au rapport des prix. La condition d’optimalité permet alors de trouver la valeur optimale 1 2 x∗ de x1. La valeur optimale x∗ de x2 s’écrit alors Prenons un exemple concret dans le cas du consommateur Soit la fonction d’utilité suivante du consommateur :U = 2xαxβ avec p1 et p2 respectivement leprix des biens 1 et 2. R le revenu. Déterminons les fonctions de demande optimales du consommateur : On a le programme de maximisation suivant : Ecriture du Lagrangien : L(x1, x2, λ) = 2xαxβ + λ(R − p1x1 + p2x2) Les CPO sont données par On a alors : Exprimons x2 en fonction de x1 : Si l’on remplace cette expression dans la contrainte nous trouverons la demande optimale de bien 1, x1∗ : Cette expression dans celle de x2 précédente nous donne la demande optimale de bien 2 pour le consommateur, soit A noter que l’on arrive exactement au même résultat si l’on procède par la méthode substitution décrite précédemment.

La méthode de Lagrange

Le multiplicateur de Lagrange est une méthode permettant de trouver les points stationnaires (maximum, minimum...) d’une fonction dérivable d’une ou plusieurs variables, sous contraintes.
Visuellement, la méthode des multiplicateurs de Lagrange permet de trouver un optimum, sur la figure ci-dessous le point le plus élevé possible, tout en satisfaisant une contrainte, sur la figure un point de la ligne rouge. Le théorème clé se conçoit aisément dans un exemple de dimension 2. 

Le point recherché est celui où la courbe rouge ni ne monte ni ne descend.

Formellement, on note comme suit l’écriture du Lagrangien :

L(x, λ) = ϕ(x) + λψ(x)

avec x les variables de contrôle figurant dans la fonction à maximiser ou de minimiser, ϕ(x) est la fonction à optimiser, λ le multiplicateur de Lagrange et ψ(x) la contrainte du programme d’optimisation.

1 Le comportement du producteur

Pour caractériser le comportement du producteur, l’analyse microéconomique suppose que l’objectif principal de ce dernier consiste à rendre son profit maximal. Le profit étant définit comme la différence entre le chiffre d’affaire et les coûts, il s’écrit mathématiquement :

avec p le prix du bien ou service produit, pQ(K, L) le chiffre d’affaire, et −wL − rK − f les coûts et plus exactement wL le coût du travail, rK le coût du capital et f la rémunération de l’ensemble des facteurs fixes de l’entreprise.

Rappel : Fonction de production : relation technique qui indique à partir de la quantité de facteurs mis en oeuvre par le producteur et la quantité maximale de produit qu’il peut obtenir.
Le comportement du producteur peut alors être appréhendé de façon différentes selon qu’il rencontre ou non une contrainte sur la quantité à produire ou sur le coût qu’il peut supporter.

(a) Le producteur contrait par son marché

Supposons que le producteur connaît le niveau maximum de production qu’il peut écouler sur le marché, il est donc contraint par les quantités et connaît à l’avance le montant de sa recette pQ(K, L).

 Dans ce cas la max du profit implique la minimisation des coûts. Donc le problème du producteur se réduit à la recherche de l’utilisation optimale des facteurs de façon à minimiser= ses coûts de production. 

Le problème s’exprime mathématiquement sous la forme d’une minimisation de coûts sous la contrainte d’un niveau de production Q

Le programme s’écrit alors : 

[post_ad]

MinC(K, L) = wL + rK + f
s.c Q(K, L) = Q

La fonction de Lagrange correspondant à ce programme est :

L(K, L, λ) = wL + rK + f − λ(Q(K, L) − Q)

Les conditions du premier ordre, qui correspondent à l’annulation des dérivées premières sont
données par :

soit : r/w = QK /QL

Avec QK et QL respectivement la productivité marginale du capital et du travail. Les deux premières équations du système des CPO permettent de définir la condition d’optimalité du producteur.

(b) Le producteur contraint par son budget

Le producteur peut se trouver dans une configuration alternative où il connaît son budget maximum. 

Les coûts ne pouvant excéder cette somme, le coût maximal de la production est connu et le recherche du profit le plus élevé possible passe par la maximisation de la recette. 

Le producteur va donc chercher la combinaison productive (K,L) qui maximise la volume de production tout en respectant la contrainte de coût.

Le programme s’écrit :   

M ax Q(K, L)

s.c C = wL + rK + f

Le Lagrangien est alors :

L(K, L, λ) = Q(K, L) + λ(C − rK − wL − f )

D’où d’après les CPO :

soit :  r/w = QK /QL 

Interprétation des conditions d’optimalité :

La résolution des deux problèmes posés par le producteur permet d’établir qu’au point optimal, la rapport des prix des facteurs doit être égal au rapport des productivités marginales. Cette égalité s’explique simplement : la productivité marginale d’un facteur rapporté à son prix correspond à la production supplémentaire obtenue en consacrant une unité de compte à l’achat d’un facteur. Par conséquent, si cette égalité n’était pas vérifiée, reporter la dépense de cette unité de compte d’un facteur à l’autre permettrait de produire plus, ce qui signifierait que la combinaison initiale n’était pas optimale.

2 Le comportement du consommateur

Le consommateur, s’il est est rationnel veut maximiser son utilité sous la contrainte d’un budget

limité afin de déterminer les quantités x1 de bien 1 et x2 de bien 2 qu’il va demander. On suppose

que l’utilité de l’agent ne dépend que des quantités de bien, ici x1 et x2.

La contrainte de budget est donnée par :

R = p1x1 + p2x2

avec R le revenu et p1x1 + p2x2 les dépenses.

Le programme de maximisation s’écrit comme suit :

M ax U (x1, x2)

s.c R = p1x1 + p2x2

Nous avons précédemment résolu les programmes d’optimisation avec le Lagrangien, nous allons maintenant montrer qu’il est possible de raisonner autrement et de procéder à la méthode dite de substitution pour résoudre ce programme.

(a) Méthode de substitution

C’est une méthode qui consiste à transformer le programme de maximisation d’une fonction à deux variables sous contrainte en un programme de maximisation d’une fonction à une variable sous contrainte.
La première étape consiste à exprimer une des variables en fonction de l’autre (par exemple x2
en fonction de x1) à partir de la contrainte 

Il faut ensuite le reporter dans la fonction d’utilité qui devient donc une fonction d’une seule

variable (ici x1).

On calcul ensuite les CPO pour trouver la valeur de x1

dU/dx1 = p1/p2 A l’optimum du consommateur le rapport des utilités marginales doit êtreégales au rapport des prix. La condition d’optimalité permet alors de trouver la valeur optimale

1                                                            2

x∗ de x1. La valeur optimale x∗ de x2 s’écrit alors

Prenons un exemple concret dans le cas du consommateur

Soit la fonction d’utilité suivante du consommateur :U = 2xαxβ avec p1 et p2 respectivement leprix des biens 1 et 2. R le revenu.

Déterminons les fonctions de demande optimales du consommateur :

On a le programme de maximisation suivant :

Ecriture du Lagrangien :

L(x1, x2, λ) = 2xαxβ + λ(R − p1x1 + p2x2)

Les CPO sont données par 

On a alors :

Exprimons x2 en fonction de x1 :

Si l’on remplace cette expression dans la contrainte nous trouverons la demande optimale de bien 1, x1∗ :

Cette expression dans celle de x2 précédente nous donne la demande optimale de bien 2 pour le consommateur, soit 

A noter que l’on arrive exactement au même résultat si l’on procède par la méthode substitution
décrite précédemment.

La méthode de Lagrange sur YouTube  

economix.fr